Finite state machine (FSM)

Andrey Dmitriev · May 8, 2021

Algorithms   C++

A finite-state machine (FSM) is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of states at any given time. The FSM can change from one state to another in response to some inputs; the change from one state to another is called a transition. An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition.

Mathematically, a FMS can be represented as A = (V, Q, S, F, d):

  • V is a input alphabet (a finite non-empty set of symbols);
  • Q is a finite non-empty set of states;
  • S is an initial state, an element of V;
  • F is the set of final states, a (possibly empty) subset of V;
  • d is the state-transition function;

Small example. We want to describe FSM for validation binary code (empty string is valid). Then we have:

  • V is any symbol;
  • Q = {q0, q1};
  • S = q0;
  • F = q0;
  • d:
    • d(q0, 0) = q0;
    • d(q0, 1) = q0;
    • d(q0, x not in {0, 1}) = q1;
    • d(q1, 0) = q1;
    • d(q1, 1) = q1;
    • d(q1, x not in {0, 1}) = q1;

And diagram:

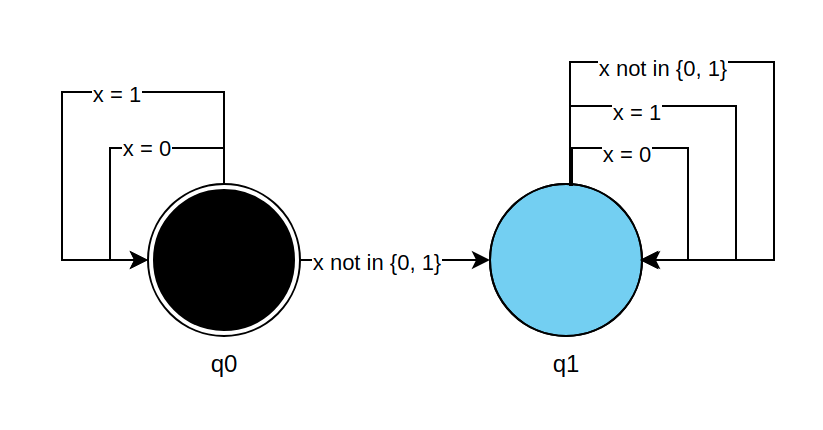
Code example

Now, we try to implement FSM for next task: validating string, which must have lowercase letter, number and special character: !@#$%^&*(). First, formilize our task!

  • V = V1 + V2 + V3;
    • V1 = {a - z};
    • V2 = {0 - 9};
    • V3 = { !@#$%^&*() };
  • Q = {q0 - q10};
  • S = q0;
  • F = q10;

Use diagram for transition:

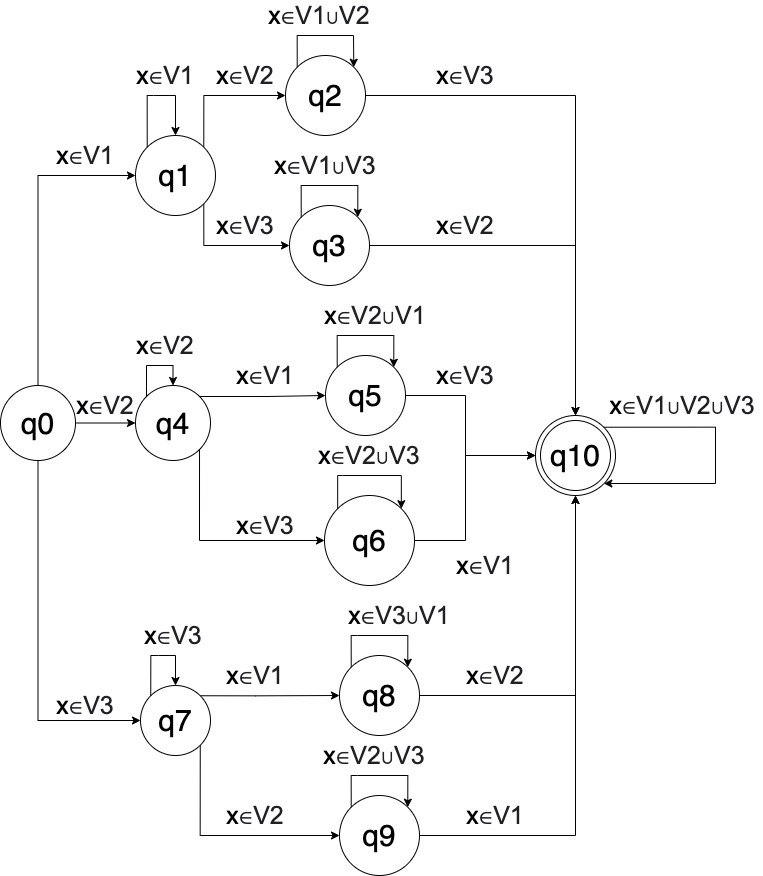
Let’s program our state machine:

#include <string>
#include <set>
#include <map>

using namespace std;

template <typename State>
class FSM
{
private:
    const set<char> &alphabet;
    const set<State> &states;
    State curr_state;
    const set<State> &target_state;
    const map<State, map<char, State>> &transitions;

public:
    explicit FSM(const set<char> &alphabet,
                 const set<State> &states,
                 State start_state,
                 const set<State> &target_state,
                 const map<State, map<char, State>> &transitions)
        : alphabet(alphabet)
        , states(states)
        , curr_state(start_state)
        , target_state(target_state)
        , transitions(transitions) {}

    bool Test(const string &str)
    {
        for (const auto &c : str)
        {
            BelongAlphabet(c);
            ChangeState(c);
        }
        return target_state.find(curr_state) != end(target_state);
    }

private:
    void ChangeState(const char &c)
    {
        try
        {
            curr_state = transitions.at(curr_state).at(c);
        }
        catch (exception &e)
        {
            throw invalid_argument("Not transition!!!");
        }
    }

    void BelongAlphabet(const char &c)
    {
        if (alphabet.find(c) == end(alphabet))
        {
            throw invalid_argument("Unknown symbol!!!");
        }
    }
};

But the most difficult job is to describe the data for constructing the FSM. Let’s do it:

set<char> set_union(const set<char> &V1, 
                    const set<char> &V2, 
                    const set<char> &V3)
{
    set<char> result(V1);
    result.insert(begin(V2), end(V2));
    result.insert(begin(V3), end(V3));
    return result;
}

enum State
{
    START_STATE, Q1, Q2, Q3, Q4, Q5, Q6, Q7, Q8, Q9, VALID
};

const set<char> V1 = {'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 
                        'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 
                        's', 't', 'u', 'v', 'w', 'x', 'y', 'z'};
const set<char> V2 = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'};
const set<char> V3 = {'!', '@', '#', '$', '%', '^', '&', '*', '(', ')'};
const set<char> V = set_union(V1, V2, V3);

map<char, State> create_transitions(State s1, State s2, State s3)
{
    {
        map<char, State> result;
        for (const auto &c : V1)
        {
            result.insert({c, s1});
        }
        for (const auto &c : V2)
        {
            result.insert({c, s2});
        }
        for (const auto &c : V3)
        {
            result.insert({c, s3});
        }
        return result;
    }
}

const set<State> Q = {START_STATE, Q1, Q2, Q3, Q4, Q5, Q6, Q7, Q8, Q9, VALID};
const State S = START_STATE;
const set<State> F = {VALID};
const map<State, map<char, State>> d = {
    {START_STATE, create_transitions(Q1, Q4, Q7)},
    {Q1, create_transitions(Q1, Q2, Q3)},
    {Q2, create_transitions(Q2, Q2, VALID)},
    {Q3, create_transitions(Q3, VALID, Q3)},
    {Q4, create_transitions(Q5, Q4, Q6)},
    {Q5, create_transitions(Q5, Q5, VALID)},
    {Q6, create_transitions(VALID, Q6, Q6)},
    {Q7, create_transitions(Q8, Q9, Q7)},
    {Q8, create_transitions(Q8, VALID, Q8)},
    {Q9, create_transitions(VALID, Q9, Q9)},
    {VALID, create_transitions(VALID, VALID, VALID)}};

And last, run it:

int main(int argc, char *argv[])
{
    if (argc == 1)
    {
        cerr << "Not arguments" << endl;
        exit(1);
    }
    string in = argv[1];

    FSM<State> fsm(V, Q, S, F, d);

    try
    {
        cout << fsm.Test(in) << endl;
    }
    catch (exception &e)
    {
        cout << false << endl;
    }
    return 0;
}

All code is here!

Of course, for such a small task, using a finite state machine is an overhead, but this is a good example for understanding how to work with them.

Twitter, Facebook