Category theory is a high level language or abstraction (the highest at this moment), that describes relationships between different objects, but does not pay attention to their structure.
Each category consists of objects and morthisms. Object is a basic element, like physical point mass. And morthisms is a mapping or transformation function between objects. Each morthism have source and target objects.
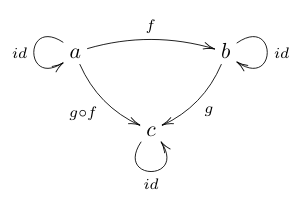Then category is a graph, which has next properties:
- Binary operation. If there are morthisms f:a⟶b and g:b⟶c, then there is morthism g⚬f or “g after f”.
- Associativity. If f:a⟶b, g:b⟶c and h:c⟶d, then f⚬(g⚬h) = (f⚬g)⚬h.
- Identity. For every object x, there exists a morphism 1x:x⟶x called the identity morphism for x, such that for every morphism f:a⟶b, we have 1b⚬f = f = f⚬1a.
Category with one object and one or same arrows is called monoid. Traditionally, a monoid is defined as a set with a binary operation. All that’s required from this operation is that it’s associative, and that there is one special element that behaves like a unit with respect to it. For instance, natural numbers with zero form a monoid under addition. Associativity means that: (a + b) + c = a + (b + c). The neutral element is zero, because: 0 + a = a and a + 0 = a.
In Haskell we have a class Monoid:
class Monoid m where
mempty :: m
mappend :: m -> m -> m
where mempty - neutral element, and mappend - binary operation.
For instance, String like monoid:
instance Monoid String where
mempty = ""
mappend = (++)